本系列文章为《High Speed Serdes Devices and Applications》的学习总结，素材主要取自教材，并附带一些自己的思考。原书下载链接：High Speed Serdes Devices and Applications.pdf

PLL（Phase-Locked Loop，锁相环）

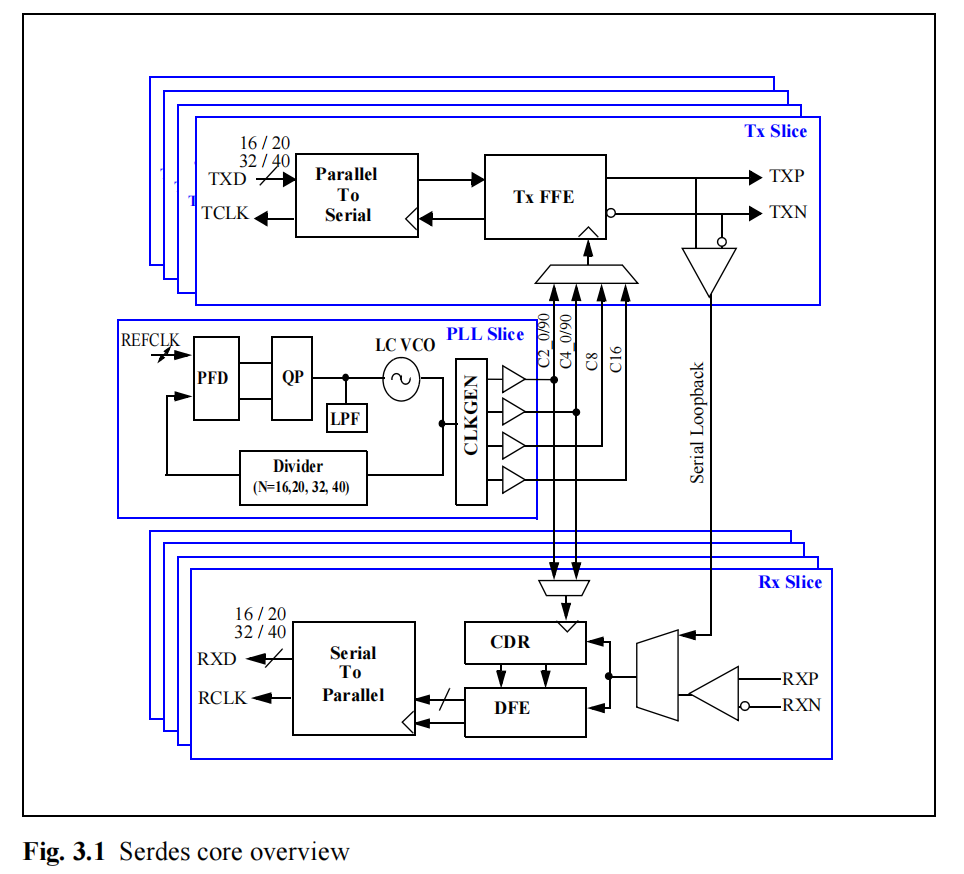
如果要粗略的分割 Serdes 的结构，那么通常可以说 Serdes Core 由 Tx 、Rx 以及 PLL 三个子模块组成，如图 3.1 所示。本文将详细介绍 PLL 的实现原理和内部结构，帮助读者理解。

PLL 的用途：

1）well-defined clock —— 需要有明确定义的时钟供系统或者模块使用，用于同步。

2）分频或者倍频时钟，可以在系统内部进行时分复用。

3）Frequency Synthesizer 频率合成器，在多载波系统中快速跳频，例如蓝牙，WiFi 通信中切换 channel。只有 PLL 能够做到低相邻载波干扰。

4）CDR（clock data recover）时钟恢复。这个也是 serdes 里面重要应用。

5）频率调制，例如 FM，FSK，QAM，OFDM 等等。

6）SSC（Spread Spectrum Clocking，扩频时钟），串行协议中的时钟频率偏移，用于降低电磁干扰（EMI，Electromagnetic Interference）。

通过输入一个参考时钟，PLL 可以输出你想要的时钟。

最简单的 PLL 结构，Simple PLL

假设有一个异或门，两个输入为 V1，V2，输出为 Vo:

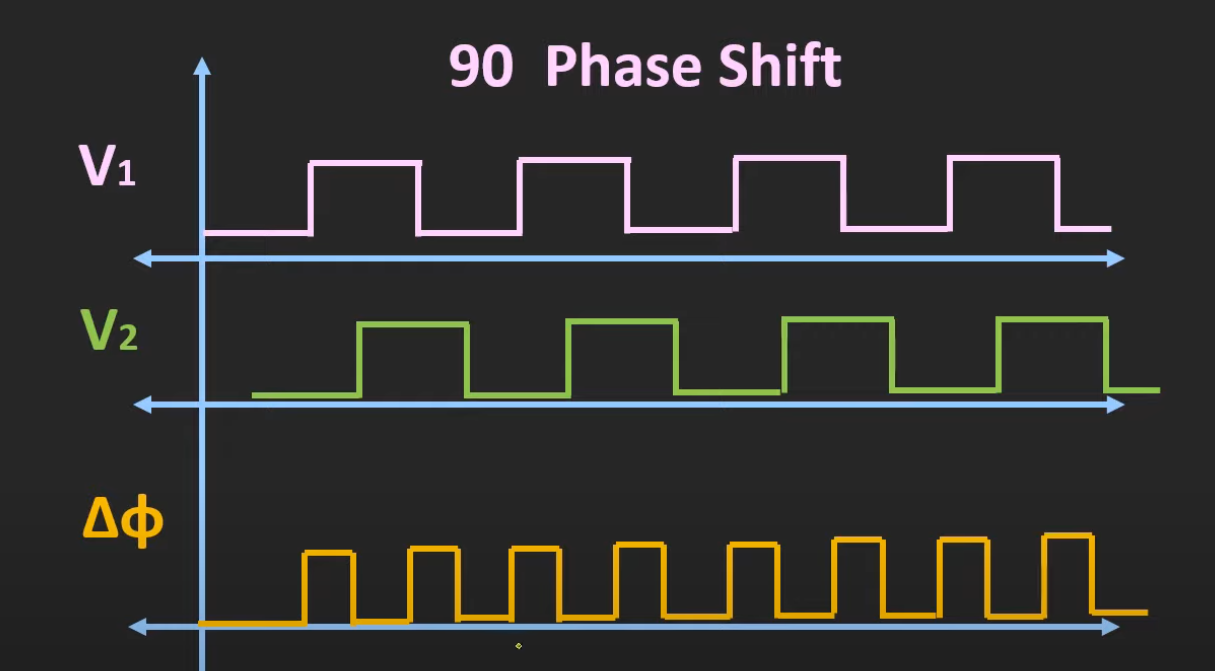
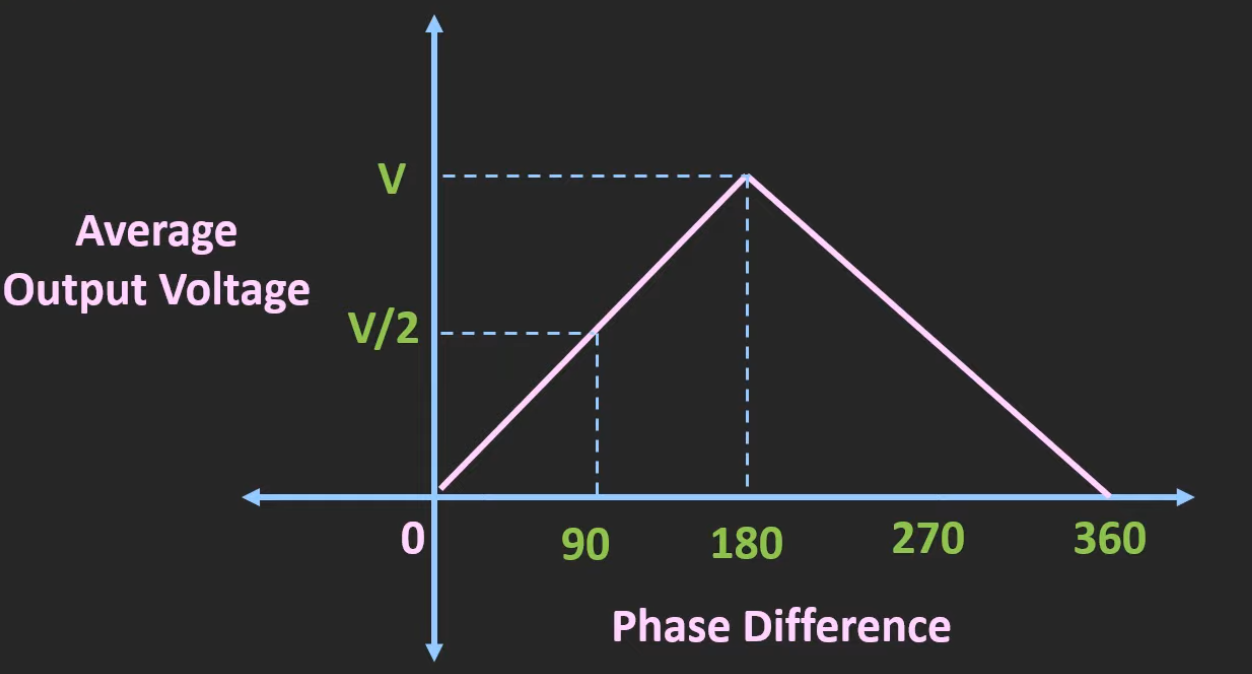
他们之间的相位关系如上图所示，让输出 Vo 经过一个低通滤波器，那么滤波后的电压可以看成平均值，这个平均电压和 V1、V2 之间的相位差是线性关系，如下图所示：

由这个输出电压来控制 VCO（压控震荡器）：

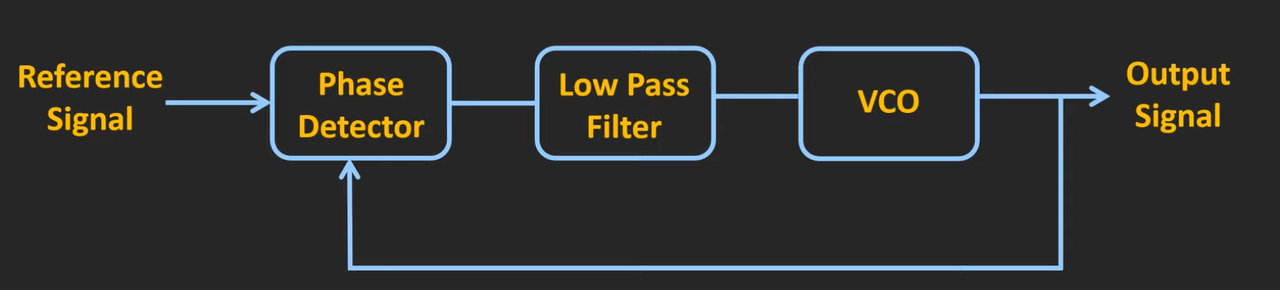
压控振荡器的输出频率和电压的关系可以看成：

fout=f0+Kvco⋅Vctrlf_{out} = f_{0} + K_{vco} \cdot V_{ctrl}

f0f_{0} 是自由震荡频率，是 VCO 没有电压输入时的频率。或者可以写为：

ωout=ω0+Kvco⋅Vctrl(t)\omega_{out} = \omega_0 + K_{vco} \cdot V_{ctrl}(t)

其中 ω0\omega_0 为自由振荡角频率， KvcoK_{vco} 为 VCO 增益。

相位检测器（PD）将相位误差 ϕe(t)\phi_e(t) 转换为电压信号Vd(t) V_d(t) ，其输出通常为 ：

Vd(t)=Kd⋅ϕe(t)V_d(t) = K_d \cdot \phi_e(t)

其中 KdK_d 为相位检测器增益。

设低通滤波器的响应函数为F(s) F(s)，则在拉普拉斯域中Vctrl(s)=F(s)⋅Vd(s) V_{ctrl}(s) = F(s) \cdot V_d(s)。

VCO 的输出相位变化率为：

dϕout(t)dt=ωout=ω0+Kvco⋅Vctrl(t)。\frac{d\phi_{out}(t)}{dt} = \omega_{out} = \omega_0 + K_{vco} \cdot V_{ctrl}(t) 。

取拉普拉斯变换，假设初始条件为零，得到：

sΦout(s)=ω0s+Kvco⋅Vctrl(s)s \Phi_{out}(s) = \frac{\omega_0}{s} + K_{vco} \cdot V_{ctrl}(s)

因此：

Φout(s)=ω0s2+Kvcos⋅Vctrl(s)\Phi_{out}(s) = \frac{\omega_0}{s^2} + \frac{K_{vco}}{s} \cdot V_{ctrl}(s)

闭环关系

  • 将 Vctrl(s)V_{ctrl}(s) 代入 VCO 方程sΦout(s)=ω0s+Kvco⋅Vctrl(s) s\Phi_{out}(s) = \frac{\omega_0}{s} + K_{vco} \cdot V_{ctrl}(s) 代入：

Vctrl(s)=Ki⋅F(s)⋅(Φin(s)−Φout(s))V_{ctrl}(s) = K_i \cdot F(s) \cdot (\Phi_{in}(s) - \Phi_{out}(s))

  • 得到：

sΦout(s)=ω0s+Kvco⋅Kd⋅F(s)⋅(Φin(s)−Φout(s))s\Phi_{out}(s) = \frac{\omega_0}{s} + K_{vco} \cdot K_d \cdot F(s) \cdot (\Phi_{in}(s) - \Phi_{out}(s))

  • 移项整理：

sΦout(s)+Kvco⋅Kd⋅F(s)⋅Φout(s)=ω0s+Kvco⋅Kd⋅F(s)⋅Φin(s)s\Phi_{out}(s) + K_{vco} \cdot K_d \cdot F(s) \cdot \Phi_{out}(s) = \frac{\omega_0}{s} + K_{vco} \cdot K_d \cdot F(s) \cdot \Phi_{in}(s)

  • 提取Φout(s) \Phi_{out}(s) ：

Φout(s)⋅(s+Kvco⋅Kd⋅F(s))=ω0s+Kvco⋅Kd⋅F(s)⋅Φin(s)\Phi_{out}(s) \cdot (s + K_{vco} \cdot K_d \cdot F(s)) = \frac{\omega_0}{s} + K_{vco} \cdot K_d \cdot F(s) \cdot \Phi_{in}(s)

  • 闭环传递函数 H(s)=Φout(s)Φin(s)H(s) = \frac{\Phi_{out}(s)}{\Phi_{in}(s)} ：

Φout(s)=ω0s+Kvco⋅Kd⋅F(s)⋅Φin(s)s+Kvco⋅Kd⋅F(s)\Phi_{out}(s) = \frac{\frac{\omega_0}{s} + K_{vco} \cdot K_d \cdot F(s) \cdot \Phi_{in}(s)}{s + K_{vco} \cdot K_d \cdot F(s)}

  • 因此：

H(s)=Φout(s)Φin(s)=Kvco⋅Kd⋅F(s)s+Kvco⋅Kd⋅F(s)+ω0ss+Kvco⋅Kd⋅F(s)⋅1Φin(s)H(s) = \frac{\Phi_{out}(s)}{\Phi_{in}(s)} = \frac{K_{vco} \cdot K_d \cdot F(s)}{s + K_{vco} \cdot K_d \cdot F(s)} + \frac{\frac{\omega_0}{s}}{s + K_{vco} \cdot K_d \cdot F(s)} \cdot \frac{1}{\Phi_{in}(s)}

稳态分析

在锁相状态下，ωout \omega_{out} 需跟踪 ωin\omega_{in}，反馈调整使 ω0s\frac{\omega_0}{s} 的稳态影响趋于零（通过Vctrl(s) V_{ctrl}(s) 补偿）。

假设输入为纯相位信号Φin(s) \Phi_{in}(s) （无ω0 \omega_0 项），则：

H(s)=Kvco⋅Kd⋅F(s)s+Kvco⋅Kd⋅F(s)H(s) = \frac{K_{vco} \cdot K_d \cdot F(s)}{s + K_{vco} \cdot K_d \cdot F(s)}

  • 这里如何理解？

稳态时，后面一项可以忽略，这里的含义是，达到稳定状态之后，VCO 的输出频率ωout \omega_{out} 就和ω0 \omega_0 无关，只受到输入频率 ωin\omega_{in} 的影响。或者说，我们这里的分析考虑的是小信号建模，Φin(s)−Φout(s)\Phi_{in}(s) - \Phi_{out}(s) 实际上会将这个自由频率带来的影响减去。

如果代入一阶低通滤波器的传递函数：

F(s)=11+sτF(s) = \frac{1}{1 + s \tau}

得到：

H(s)=Kvco⋅Kds2τ+s+Kvco⋅KdH(s) = \frac{K_{vco} \cdot K_d}{s^2 \tau + s + K_{vco} \cdot K_d}

这就说明整个 PLL 的传递函数H(s) H(s) 可以看成是一个二阶的低通滤波器。也就是说，如果输入信号频率（相位）突变，输出会缓慢跟随直至相等。具体是怎么恢复到稳态，与低通滤波器和 VCO，PD 属性有关，即过阻尼，欠阻尼，临界阻尼三种跟随方式。

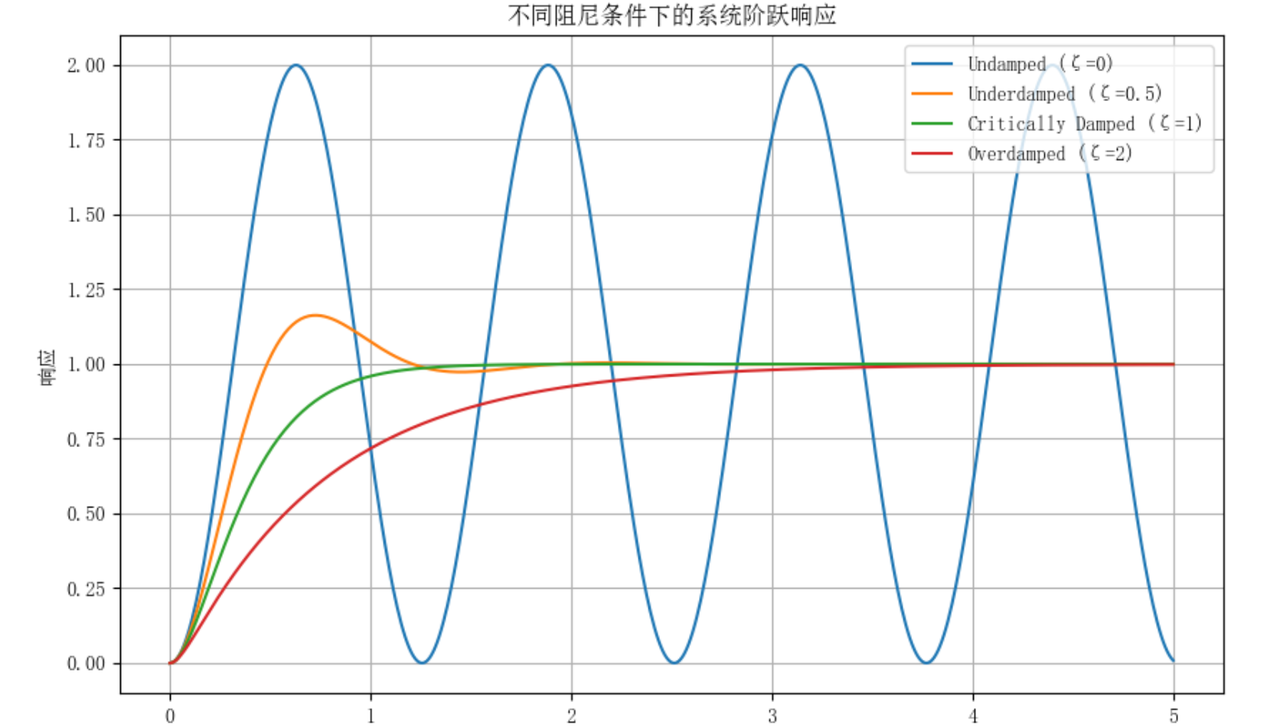
图中通过欠阻尼 (ζ<1) 和过阻尼 (ζ>1 ) 的响应曲线，揭示了 PLL 设计中的动态性能与稳定性的矛盾，总结如下：

  • 欠阻尼 (ζ<1)：

    • 特性：响应曲线显示振荡（"Wants rings to settle"），即输出 ωout\omega_{out} 在跟踪ωin \omega_{in} 时出现过冲和振荡，最终收敛。

    • 问题：振荡可能导致相位噪声或频率不稳定，尤其在高速跳频（如 RF/Wireless/mmWave 应用）中，影响信号质量。

    • 应用场景：适合需要快速响应的场景，但牺牲了稳定性。

  • 过阻尼 (ζ>1 )：

    • 特性：响应曲线平滑上升（"Wants settle"），无振荡，但收敛较慢。

    • 问题：缓慢的上升时间可能无法满足快速通道切换的需求，尤其在无线通信中要求快速频率调整。

    • 应用场景：适合需要稳定性的场景，但牺牲了响应速度。

总结异或门 + 低通滤波器的具体问题

  • 异或门作为相位检测器：

    • 异或门输出与相位差 ϕe\phi_e 成线性关系，但其增益 KdK_d 较低，且对大相位误差（> π ）非线性，限制了锁相范围。

    • 低增益导致 Kvco⋅KdK_{vco} \cdot K_d 较小，环路带宽窄，动态响应较慢。

  • 低通滤波器 (LPF)：

    • LPF 滤除高频噪声，但若截止频率设计不当（太低），会进一步减慢响应；若太高，则无法有效抑制振荡。

这也说明了这种结构的 Simple PLL 存在着以下问题：

  • 稳定时间和抖动之间的矛盾。

  • Phase 之间的关系不确定，随着温度电路改变。

  • 存在稳定性问题，即欠阻尼下过冲震荡。

  • 不知道锁定范围有多大，与回路带宽有关。

——————————————————————————————————————————

参考链接：李致毅教授 B 站视频：鳌中堂讲电路

图片部分来源：What is Phase Lock Loop (PLL)? How Phase Lock Loop Works ? PLL Explained